The day was June 3rd, 1997; Brazil was playing France in a football World Cup warm-up tournament. 24-year-old Roberto Carlos was 35 metres out, and the blue wall of French defenders in front of him looked formidable. Carlos lined up for the free kick, starting with a run up from far back; as he struck the ball, it went far out to the side of the defenders. Surely it was off target—a ball boy standing well to the right of the goal even ducked, thinking it would hit him. Then, almost magically, the ball swung mid-air, curving left smoothly into the goal! The goalkeeper was so astonished, he could only stop and stare.
Carlos taking the famous free kick (picture credits fourfourtwo.com)
This is the famous “banana kick”, and Carlos’ goal is the most notorious
example of it. The banana kick has perplexed players and pundits alike, and a
team of French scientists even wrote a paper on the mechanics of it. But what
exactly is happening here? How does the ball, which is kicked in what seems to
be a straight line, hook in the air? It seems fantastical, almost as if the ball has a
mind of its own, avoiding the defenders and then making a beeline right for the
goal… but that, of course, is not what is happening here.
The curious trajectory of this ball is down to what’s called the Magnus effect,
which itself is a manifestation of a more general theorem, Bernoulli’s theorem.
This is a theorem that most of us would have studied at least at the high school
level. Bernoulli’s theorem is essentially a statement of the conservation of
energy in a flow field. It states that within a fluid, an increase in speed coincides
with a decrease in static pressure or potential energy. In equation form, it can be
represented as seen below (this is the equation at any point along a streamline):
\(𝑝 +\frac{𝜌𝑣^2}{2}+ 𝜌𝑔ℎ = 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡\)
where p=pressure at the specified point, ρ=density of the fluid at all points,
v=fluid flow speed at the point, g=acceleration due to gravity and h=elevation
of the point above a reference.
The Bernoulli principle has applications in many areas of modern life, from
aeroplane design and aerodynamic lift to measuring the flow speed of a fluid.
However, we’re interested in a slightly different application: sports! To
understand the famous banana kick, however, we’ll first have to look at one
manifestation of Bernoulli’s theorem, called the Magnus effect.
The Magnus effect is a phenomenon most commonly associated with spinning
objects moving in fluids (for example, a football). The crux of the effect is that
the spinning object demonstrates a deflection in trajectory that is not replicated
with non-spinning objects; we saw this in Carlos’ kick, where the trajectory of
the ball looked almost banana-shaped. So, what is happening here? From
Newton’s first law of motion, we know that the ball’s deflection must be due to
some force changing its velocity. The Magnus effect accounts for exactly this
force, which we call a “pressure-gradient force”.
The explanation for the effect is as follows: the ball is travelling in a certain
direction, and spinning around an axis perpendicular to that direction.
Meanwhile, the fluid around the ball is flowing in the opposite direction to the
ball’s motion. Since the ball is also spinning, the result is that on one side of the
ball, the flow of fluid is in the same direction as the spin of the ball, while on
the other side, the flow is opposite to the spin. We can see this in the figure.
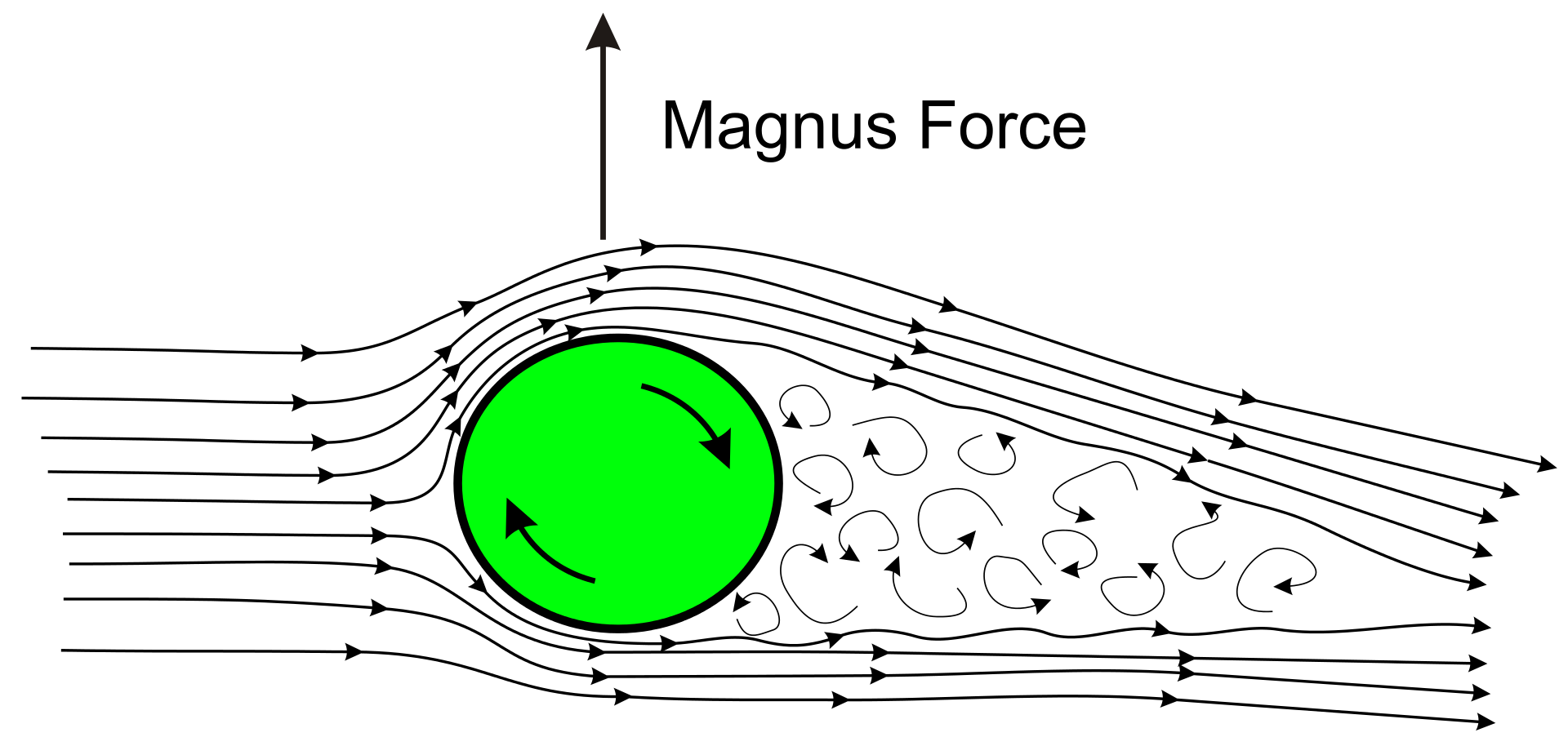The Magnus effect (picture credits Wikipedia)
From Bernoulli’s theorem, we can understand how this difference between the
two sides creates a pressure differential; the side where the directions of spin
and flow are the same is at a lower pressure than the side where the directions
are opposed. This pressure gradient, in turn, produces the effective “Magnus
force”. This causes the ball to turn, moving towards the direction of the lower
pressure zone.
Now, when Carlos took his free kick on that day in 1997, he kicked the ball near
the bottom right, which imparted not just translational velocity, but also
rotational motion. It wasn’t just moving in a straight line; it was spinning
around its own axis as well. This spin gave rise to a pressure-gradient force that
resulted a curving trajectory, so the ball went out around the defending wall and
back inwards as it flew into the goal. This free kick, so often hailed as
miraculous, can be neatly explained by one of the most important principles of
fluid dynamics.
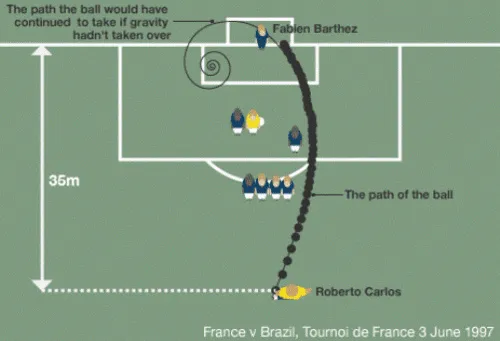Carlos’ kick (picture credits ESPN)
Of course, Carlos was not an expert on the finer details of Bernoulli’s theorem,
but he did have an intuitive understanding of the motion of the ball. He took
advantage of the wind direction and his months of practice, imparting just the
right angular velocity for the ball to reach the goal. He had been practising this
kick for years, and later remarked that that moment was probably the proudest
of his career. That particular shot was voted Goal of the Decade recently.
The Magnus effect, meanwhile, explains a lot of other sporting phenomena:
from the slightly extended trajectory of a golf ball, to the crazy spin of a table
tennis ball. Sports fans might see curving trajectories or unlikely shots as
miraculous or magical, but there’s a scientific explanation for each of them: we
just need to look. So, the next time you see something on TV or in your life that
looks like it defies the laws of physics or probability, stop for a minute and
think about whether it actually does—or if there’s something far more complex
and fundamental going on than a fluke or a miracle.
References
Roberto Carlos’ Brazil free kick in 1997: The physics behind ‘impossible’ strike
Football physics: The “impossible” free kick - Erez Garty
