Before we get into why it is interesting, let me tell you what a cycloid is. A curve traced by a point on a circle being rolled around a straight line is called a cycloid. The first interesting property that strikes us is that this curve isn’t part of a circle! As you will see, this is just the starting of the many interesting properties. Using elementary mathematics, we can show that the equations governing a cycloid are:
\[x = a(t-\sin t) \\ y = a(1-\cos t)\]Brachistochrone
Have you ever wondered how quickly a small ball could descend from one point to another? What if one wanted to find the quickest possible path? You might think that this is a no-brainer and conclude that the answer has to be a straight line. However, that is the path of least distance and not quickest. Due to gravity, the ball’s speed increases as the steepness of the path increases. After this thought, we can understand why the path has to be some curve. What does this curve look like? What are its properties? Can we find the exact equations governing this curve?
This isn’t the first time one has asked these questions. In fact, Johann Bernoulli asked these very questions in 1696. Since then, many ingenious solutions have been found. The solution is a curve which is called the Brachistochrone curve. Interestingly, this curve is part of a bigger curve which you might’ve guessed by now is the cycloid. Bernoulli’s solution to the problem uses Fermat’s principle, which states that light always travels in the path which takes the least time. So, he considered light’s trajectory in a medium where its speed varies with gravity in accordance with energy conservation. On the other hand, Newton’s solution gives us a better understanding of why the cycloid is the solution. It places conditions on the normal forces at each point on the curve, which is satisfied by a cycloid.
A real demonstration of how the Brachistochrone (middle) fares against other trajectories (Courtesy: Vsauce - The Brachistochrone)
Bernoulli used energy conservation to get the constraint where \(x\) is the vertical distance fallen, given by \(v^2 = (constant)\ x\). With this constraint, he obtained the “refractive index” as a function of the distance fallen. Applying Snell’s law to this setup and setting the constant above as \(2a\), he got:
\[dy = dx\sqrt{\frac{x}{(2a-x)}}\]This relatively simple differential equation can be integrated easily using the substitution method to yield the equations at the beginning of this article. It is a rumour that Bernoulli recognized that this is the differential equation for a cycloid even before solving. Talk about intuition!
Tautochrone
Cycloids are the solutions to another interesting problem. This is known as the Tautochrone problem. This question asks us to find the curve for which the time taken by an object sliding without friction in uniform gravity to its lowest point is independent of its starting point on the curve. Isn’t that mind blowing?! There are two paths. One is a subpart of another. Still, an object falling through them will take the same time to go through them!! Extremely precise changes in speeds with distance make this possible. It is these kind of fascinating observations that make one find beauty in the simplest shapes around us.
There isn’t an explanation which is as intuitive and easy as for the previous question. However, if you are interested in the solution, do go through this concise explanation and the sources therein.
This was first discovered by Christiaan Huygens in 1659. It is mind-blowing for cycloids to be the solution for this problem as well. You might be confused as to how both these different questions have the same solution. However, the Brachistochrone curve is only a part of the cycloid (can be any part), and the Tautochrone curve is the entire cycloid. This property can be understood by looking at isochronous cycloidal pendulums. As you might have heard, the time period of a simple pendulum is independent of its amplitude under a small angle approximation, but in the case of a cycloidal pendulum, it holds true for any angle (amplitude). Cycloidal pendulums are used in making highly accurate timed clocks. Here is an insight of how they work:
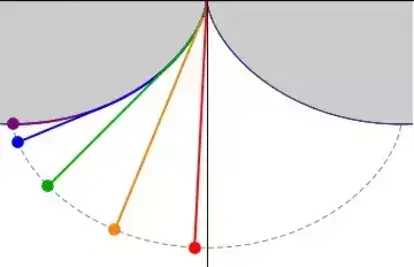5 cycloidal pendula with different amplitudes. As we can see, the time period of all the pendula is same (Courtesy: Wikipedia)
OK… but why do we care?
While appreciating its beauty, you might now start to wonder about the purpose of studying this curve. This particular curve finds itself in many places. For example, it is used in violin plate arching and by architects for aesthetic purposes. You can also find them in amusement parks; the carriages in roller coasters need to gain high speeds in a short amount of time. Hence, the shape of the tracks is, more often than not, a Brachistochrone curve. It is frequently found in mechanical engineering since it is constantly found in parts of machines as it is so intimately related to circles. It is also crucial to learn about this curve so that we can understand its cousins (trochoid, hypocycloid, epicycloid, epitrochoid, hypotrochoid to name a few) better. These curves have a lot more applications in engineering fields like in rotary pumps.
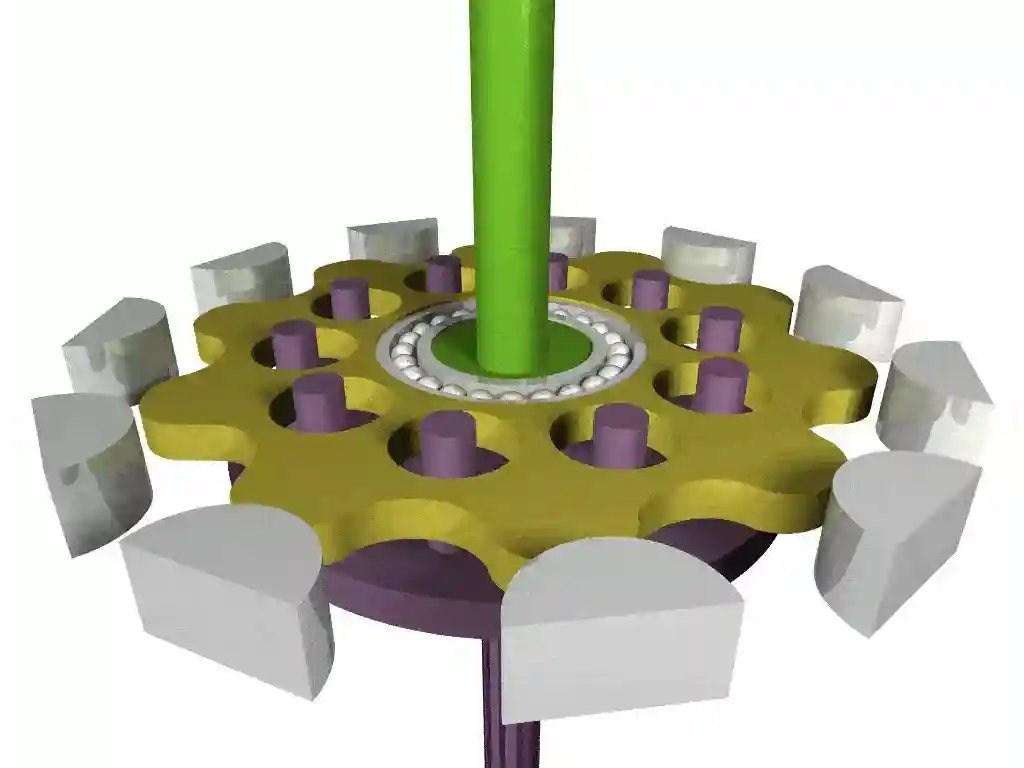Cycloidal gear in motion (Courtesy: Wikipedia)
Even though it has a lot of applications in the real world, studying it is an intellectual pursuit. It is questions like this that allow people to think originally and creatively so that we can make progress in a broad range of fields and give various results. Some of these results find applications while others don’t (for the time being!), but being the inquisitive creatures we are, no other reason is needed for us to unravel any mystery.
References:
Edited by Aniket Kukreti
