Type Ia supernovae (SNIae), observed to be caused by the detonation of a white dwarf star, are generally a very consistent type of stellar explosion that make up a significant part of the distance ladder. Their consistency even led us to discover dark energy! However, more and more unique examples of SNIae have been discovered, and this has led researchers to question our understanding of the physics behind SNIae. This article looks at how the presence of a magnetic field could impact the types of SNIa explosions that we see.
White dwarf stars accompanied by a binary partner tend to accrete mass over a period of time. As white dwarfs grow in mass, they experience a stronger gravitational force that drives the star towards collapse. We know that the white dwarfs are supported against the gravitational collapse by the electron degeneracy pressure. However, electron degeneracy can battle against only a limited amount of gravitational pressure.
S. Chandrasekhar was awarded the 1978 Nobel prize in Physics for calculating the maximum white dwarf mass, 1.4 \(M_{\odot}\), that electron degeneracy pressure could withstand. When the total mass of a white dwarf crosses this limit, a thermonuclear runaway reaction is ignited and the star is torn apart in a dramatic explosion. These explosions are some of the brightest events in the universe! Within a timescale of 15-20 days, they can release as much energy as our sun will produce in its entire lifetime.
Artist renditions of two different formation mechanisms for a SNIa. Left: Collision of two white dwarfs, producing a SNIa through the double degenerate scenario. Right: The single degenerate scenario, in which a white dwarf accretes matter up to the Chandrasekhar mass limit and then explodes. Images taken from Wikipedia Commons and Discover Magazine.
It’s thought that all of the carbon-oxygen (the most common type) white dwarfs explode when they cross the 1.4 \(M_{\odot}\) limit. Similar composition and the same amount of mass imply SNIae all release roughly the same amount of energy in their explosions over a similar timescale. Therefore, any SNIa would give rise to roughly the same light curves once it is properly calibrated. The distance to the explosion can be measured based on the calibration. Hence, the SNIae explosions are also called standard candles.
However, what if some exotic phenomenon could change the Chandrasekhar mass limit? We have observed SNIae with greater than expected luminosities(the superluminous SN Ia). These superluminous SNIae , need a progenitor white dwarf of 2.1-2.8 \(M_{\odot}\) in order to match observations.Research into the nature of highly magnetized white dwarfs, has led to the discovery that some white dwarfs could indeed hold mass beyond 1.4 \(M_{\odot}\), even up to 2.8 \(M_{\odot}\) sometimes. These advances question the standard candles we have used until now and also provide a possible explanation for the progenitors of superluminous SNIa’s.
Artistic sketch of a white dwarf and its magnetic field lines. Image taken from American Astronomical Society NOVA.
Research led by Professors at Department of Physics of Indian Institute of Sciences, looked into the fundamental properties of highly magnetized white dwarfs, to find out the problems leading to superluminous SNIa and Chandrasekar mass limit violation. In the paper, the authors look at how changes in the Equation of state for white dwarfs could alter the mass limit. An Equation of state (EoS) relates the pressure and the density within the stellar core. The mass and radius of a star can then be calculated using this equation.
The original Lane-Emden EoS did not take into account the magnetic field. A white dwarf establishes hydrostatic equilibrium based on the quantum effects of degenerate electrons. Very high magnetic fields are known to change the available energy states of such degenerate electrons. ‘Landau quantization effects’ summarizes the effects of magnetic fields on degenerate electrons, and brings in Landau levels (energy levels of degenerate electrons in a magnetic field). Without the presence of a magnetic field, all the Landau levels are occupied (see the following figure for illustration). As the magnetic field grows in strength, fewer Landau levels are available for electrons. Changes in electron levels alter the degeneracy pressure, consequently changing the density and the EoS for the white dwarf.
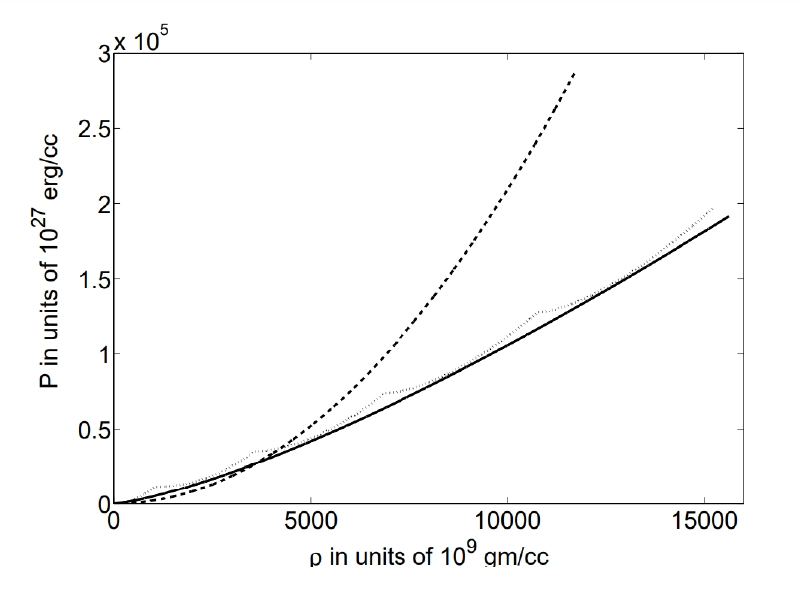Plot of equations of state — the x-axis shows the density, and the y-axis shows the pressure. The solid line represents Chandrasekhar’s equation of state with zero magnetic field and therefore infinitely many Landau levels. The dotted and dashed lines represent a white dwarf with 5 Landau levels (corresponding to a strong magnetic field) and a white dwarf with 1 Landau level (corresponding to an extremely strong magnetic field) respectively. A stronger magnetic field allows for more electron degeneracy pressure support. Figure taken from this paper.
For Landau quantization to come into effect, magnetic fields of \(~10^{15} G\) are required. Now, most white dwarfs have surface magnetic fields of no more than \(10^{10} G\), which is much less than \(~10^{15} G\). But as the matter density increases towards the core of the white dwarf, the magnetic field near the core also increases sharply due to conservation of magnetic flux. Moreover the SNIae progenitors are accreting white dwarfs. With an increase in accreted mass, gravitational pressure increases, and consequently, the white dwarf shrinks. In other words, as the size of an accreting white dwarf decreases with a rise in its total mass, the conservation of magnetic flux in such compact objects leads to an increase in the magnetic field strength at the center. As shown in Figure 3, a strong central magnetic field allows for more outward pressure support from electron degeneracy, allowing for the white dwarf to survive higher inward gravitational pressure and grow beyond 1.4 \(M_{\odot}\).
The Chandrasekhar mass limit was formulated without considering magnetic effects, but current observations mean that high magnetic fields cannot be neglected. The EoS derived after considering just one (the zeroth) Landau level leads to a new ultimate mass limit for white dwarfs of about 2.58 \(M_{\odot}\). White dwarfs with lower magnetic fields can have multiple Landau levels leading to their maximum mass lying between 1.4 and 2.58 \(M_{\odot}\). White dwarfs with insignificant magnetic fields will tend to have infinite landau levels and exhibit the usual Chandrasekhar mass limit. This consideration of new mass limits and above the Chandrasekhar limit might explain the occurrences of superluminous white dwarf explosions and could lead us to redefine the SNIa standard candle!
References
- Das, Upasana, and Banibrata Mukhopadhyay. “New Mass Limit for White Dwarfs: Super-Chandrasekhar Type Ia Supernova as a New Standard Candle.” Physical Review Letters, vol. 110, no. 7, Feb. 2013, p. 071102.
- Srinivasan, Ganesan. Life and Death of the Stars. Springer Science & Business Media, 2014.
- Branch, David, and J. Craig Wheeler. Supernova Explosions. Springer, 2017.
- Alsabti, Athem W., and Paul Murdin, editors. Handbook of Supernovae. Springer International Publishing, 2016.
