Article Series: Women in Science
If I ask you to name a few mathematicians (and theoretical physicists) who changed the course of human scientific thinking and understanding, then who shall be there in your list? Newton and Einstein shall be there for sure. There may be Gauss, Euler, Riemann, Maxwell and even Schroedinger. If I still press on, you might think a bit more harder and you may murmur names of Hawking and Feynman. But, what if I tell you that you missed the name of one of the most important human beings who ever lived on the planet? And this person, undoubtedly one of the brightest jewels of humanity was a woman and probably the greatest unsung hero of science!
She is Amalie Emmy Noether.
Emmy Noether (1882-1935) [Courtesy: Wikipedia]
The Beginning
Born in a German Jewish family in late 19th century, Noether’s life period was a time when women were restricted access to academia and also when anti-semitism was rising to its peak in Germany. In short, the world gave her nothing but obstacles. But she gave the world a lot: from one of the most powerful theorems in physics to immense wealth of knowledge and understanding in abstract algebra. One of the most brilliant minds that humanity has ever produced, Emmy Noether was mostly unrecognized throughout her life and also by her immediate posterity; she wasn’t given a full professorship post in any university and for a long period she had to lecture without any pay! The life of this amazing person is that of struggle against society, and also that of love towards the truth and beauty of science.
She was born in the year 1882 to Max Noether and Ida Amalia Kaufmann. Her father, Max Noether was a leading mathematician at the University of Erlangen. She developed interest for mathematics since an early age and instead of getting a “very good” overall grade in examination for teachers in English and French and thereby qualifying to teach these languages at schools reserved for girls, she instead chose to continue her education at University of Erlangen in 1900. Being a girl, she was only allowed to audit the courses and that too after getting permission of the respective course professors. Despite of all the restrictions, she passed the graduation exam in 1903 with flying colours. She then briefly went to Gottingen in winter of 1903-1904 and among her lecturers there were Felix Klein and David Hilbert, the people who would invite Noether to Gottingen a decade later to help them solve an apparent puzzle regarding Einstein’s General Relativity. In 1904, she returned back to Erlangen for Ph.D. and under the supervision of Paul Gordan, completed her dissertation in 1907.
Having demonstrated considerable mathematical talent (although this wasn’t even the trailer for the film to come), if Noether had been of the other gender, Noether’s career would have sky-rocketed at an unprecedented rate. But being a woman, she was denied a paid teaching post at Erlangen and was only given to lecture at University of Enlargen’s Mathematical Institute without any pay, often as a substitute for her sick father. She lectured there for seven years and in the spring of 1915, she was invited to return to Gottingen by Hilbert and Klein. They wanted to recruit her as a paid faculty but the decision was vehemently opposed by the faculty senate. In response to one of the faculty member’s protest on recruiting a female professor, Hilbert had said that, “we are a university, not a bathhouse!” However, inspite of the sincere efforts of these two great mathematicians, Noether wasn’t given a paid professorship post and had to lecture as an “assistant” under Hilbert.
The Magnum Opus
In 1918, Noether published an important theorem connecting symmetries in nature with conservation laws. The theorem, which now bears her name is according to many, one of the most beautiful theorems in physics which has propelled the development of physics throughout twentieth century and still continues to underpin our present understanding of the physical universe.
So, what does the theorem exactly say? Understanding the theorem requires knowledge of Lagrangian formulation of mechanics. In short, the Lagrangian formulation is a departure from Newtonian formulation in terms of foundational principles. In this formulation (also called variational formulation), we deal with the problem of finding the real trajectory of the system as it moves from one point (or one configuration) to another point (or configuration) in some given time. There is a quantity called “action” that can be defined along each possible trajectory between the two points (which is actually the time integral of the Lagrangian along the trajectory) and the system shall follow that trajectory (or in some cases, the system of trajectories, where the precise trajectory shall be picked up by initial conditions) along which this action shall be “stationary” (in general action is least, or, in some cases, it is a saddle).
Using calculus of variations, it can be shown that the trajectory that the system follows is the solution of Euler-Lagrange equations with given intial conditions. Here comes the good part: if this action itself has a symmetry (more precisely, a continuous global symmetry) under infinitesimal transformations, then there is a corresponding conserved quantity along the solution trajectory. Moreover, the theorem not only tells that there exists a conserved quantity, but it also gives an explicit prescription of the conserved quantity.
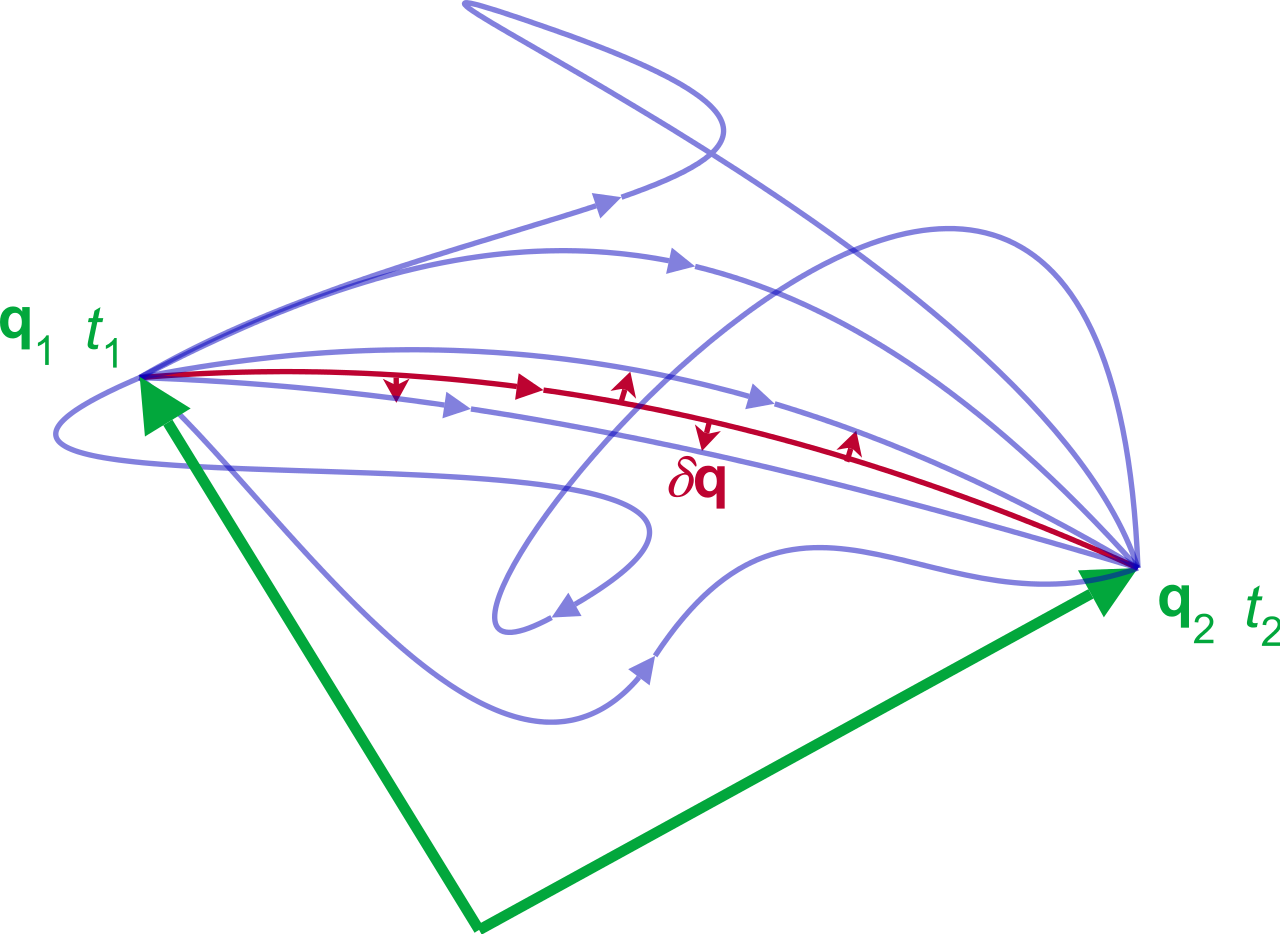An accompanying visual for the principle of least action
The paragraphs above may feel extremely vague if you haven’t studied some advanced theoretical mechanics, but the beauty and power of the theorem can be easily demonstrated in a slightly non-rigorous way. Consider a pendulum swinging in vacuum under gravity. It will continue swinging forever as energy is conserved. Then, by virtue of Noether’s first theorem (there are actually two Noether’s theorems, we are only concerned about the first one here), the action of the pendulum is symmetric under time translation. This actually signifies that the laws of nature governing pendulum motion do not change over time. What a wonderful insight! Energy conservation is exactly same as stating that laws of nature are invariant over time! Similarly, space translational symmetry gives rise to conservation of linear momentum, rotational symmetry leads to conservation of angular momentum and the list continues to more exotic symmetries and conserved quantities. Surpassing classical mechanics, this powerful theorem is applied in quantum mechanics, field theories and has guided our present understanding of fundamental particles and interactions between them at all steps. Just imagine what a magnificient leap in understanding it was!
Beyond Noether’s Theorem
The German revolution of 1918-1919 brought some changes in social attitude towards women. Three years later, she was granted “extraordinary” professorship post at Gottingen, which though sounds prestigious, was an unpaid post and only a year after that she was given a paid special position of lecturer.
Her works in abstract algebra carried out by her 1920 onwards is now considered absolutely fundamental which played crucial role in the development of this budding mathematical discipline. Abstract algebra is that branch of mathematics which deals with algebraic structures like groups, fields, rings, modules and their properties. She also paved the way for application of algebra in topology leading to the birth of algebraic topology. In this article, we shall not be dealing about her great contributions in these areas, but it is worth noting that she spent most of her life as an “algebraist” making groundbreaking discoveries in these areas.
Prof. Noether with mathematicians at Göttingen, 1931 (Courtesy: National Library of Israel)
In 1932, she and Emil Artin (for the math folk reading this, Emil Artin is the father of MIT professor Michael Artin, the author of the super-famous textbook “Algebra”) received Ackermann-Teubner Memorial Award. However inspite of that, she was not elected into Gottingen Academy of Sciences and was never promoted to the post of full professor. In September of the same year, she was invited as a speaker at the International Congress of Mathematicians at Zurich.
Curtain Call
With the rise of Nazi activity in Germany under the leadership of Adolf Hitler, she was expelled from the University of Gottingen in April 1933 due to her being of Jewish descent. She left Germany and took refuge in the United States. She took a teaching position at Bryn Mawr’s College in Pennsylvania in late 1933.
In April 1935 she got diagnosed with a pelvic tumor. During operation, the doctors discovered an ovarian cyst and two small tumors in the uterus. Due to some complications in surgery followed by an infection that probably affected heat centers at the base of her brain, she suddenly fell unconscious on 14th April and her temperature soared to about 109°F, followed immediately by death at just the age of 53.
A Formidable Legacy
Although she left the world at an early age, her contributions continue to live on. The fundamental insights that she brought and the powerful new principles that she formulated still continues to propel theoretical physics and mathematics. While most of the mortals of her time failed to give proper respect and recognition to her, she always roamed in the uppermost echelons of mathematical sciences, probing deeper principles of nature and composing her mathematical music: a symphony that shall continue to resonate through ages reminding the posterity of this great ornament of the human race.
She is immortal, as her works are so fundamental that,
“So long as men can breathe or eyes can see,
So long lives this, and this gives life to thee.”
~ (Couplet of Sonnet 18, William Shakespeare)
References
- Emmy Noether’s Wikipedia page
- Biography: Emmy Noether
- Mechanics: Third Ed. Course of Theoretical Physics Vol. 1: L.D. Landau and E.M. Lifshitz
Edited by Aniket Kukreti
