The 2-Hour Rule: A Hidden Rhythmic Constraint in the Cosmos
A few days ago, someone I know casually dropped an interesting fact:
“It takes 2 hours to orbit at the surface of any object made of rock.”
At first, I was skeptical. Earth’s low orbit takes just 1.5 hours, not 2. But then it hit me - Earth isn’t just made of rock. It has a dense iron core, which increases its gravity and shortens its orbital period.
Still, the number 2 seemed oddly simplistic and too good to be true. Could it be a coincidence? Nope ! It turns out this is (almost?) a fundamental rule of physics.

The Simple Math Behind the 2-Hour Rule
We can prove this rule using basic physics. The time it takes to orbit an object depends on its density, not its size.
The formula for an orbital period just above the surface of an object is:
\[T_c = \frac{C}{v_c} = \frac{2\pi R}{\sqrt{\frac{GM}{R}}}\]With Mass being:
\[M = \frac{4}{3} \pi R^3 \rho\]Combining the two:
\[T_c = \frac{2\pi R}{\left(\frac{G}{R} \cdot \frac{4}{3} \pi R^3 \rho \right)^{1/2}}\]Simplifying more:
\[T_c = \frac{2\pi R}{\left(\frac{4\pi}{3} \right)^{1/2} (G \rho)^{1/2} R}\]Which turns out to be:
\[T_c = \sqrt{\frac{3\pi}{G \rho}}\]This equation tells us something amazing:
- The time it takes to orbit only depends on density.
- The radius and mass of the object don’t matter at all!
When we plug in the density of rock (~2700 kg/m³), we get:
\[T_c \approx \sqrt{\frac{3\pi}{6.67 \times 10^{-11} \text{N} \cdot \text{m}^2 / \text{kg}^2 \times 2700 \text{kg/m}^3}}\] \[T_c \approx 7232 \text{ s} \approx 2.01 \text{ hrs}\]That’s why all large rocky asteroids follow the 2-hour rule - it’s built into the laws of gravity!
Proof from Real Asteroids
This isn’t just a math trick. Astronomers have measured the distribution of asteroid rotation speeds vs their size
- A study by Hu et al. (2021) analysed thousands of asteroid spin rates.
- Here’s a plot of the data:
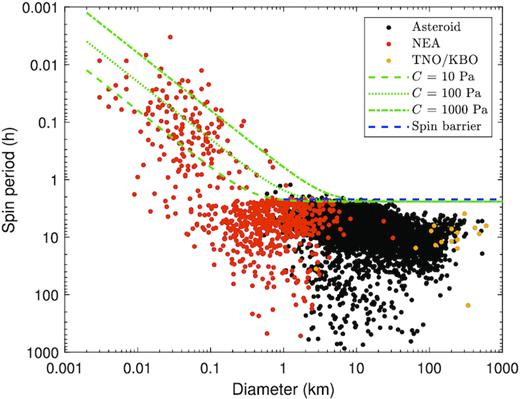
Notice the cutoff? Above a certain size, there are no asteroids that spin faster than once every 2 hrs.
Is this a coincidence? Nope! Same physics. Most asteroids are mostly rock, and once they get big enough to be held together by their own gravity, if they were spinning faster than once every 2 hours, then parts of them would (by definition) be in orbit. Material would get thrown off their equator until the asteroid shrank/spun down to the 2 hours period limit.
What This Data Tells Us:
- No large asteroid spins faster than ~2 hours - proving the spin barrier.
- Small asteroids (<200m) can rotate faster - because they are solid rocks, not rubble piles.
- The green lines show how different material strengths affect the limit.
Why Do Small Asteroids Break the 2-Hour Rule?
Some small asteroids do spin faster than 2 hours. How? They aren’t rubble piles - they are solid monolithic rocks.
For example:
- Asteroid 2008 TC3 (4 meters wide) spun once every 90 seconds!
- Asteroid 2017 QG (5 meters wide) spins in just 30 seconds!
💡 Conclusion: Small asteroids can spin fast because they are held together by rock strength, not gravity.
Beyond Asteroids: A Universal Rule?
This isn’t just about asteroids. The 2-hour rule works for any object in space, and it depends only on density.
| Material | Density (kg/m³) | Orbital Period |
|---|---|---|
| Rock | ~2700 | 2.0 hrs |
| Metal | ~7000 | 1.2 hrs |
| Ice/Water | ~1000 | 3.3 hrs |
| Gas Giants | ~1400 | 2.8 hrs |
Let’s check some real planets and moons:
🌎 Earth: 1.5 hrs
🌔 Moon: 2.0 hrs
🔴 Mars: 1.8 hrs
Even though these objects are of different sizes, their orbital periods match their densities!

Asteroid Psyche is a large, metal-rich asteroid located in the main asteroid belt between Mars and Jupiter, composed primarily of iron and nickel, similar to Earth’s core. How much do you think it’s spin period would be?
What About Small, Fast-Spinning Asteroids?
A later study, “Critical spin periods of sub-km-sized cohesive rubble-pile asteroids” (arXiv:2009.12605), explains why some small asteroids spin faster than 2 hours.
The crux being:
- If an asteroid is small enough, it can hold itself together using weak forces.
- Even tiny cohesion (like weak glue) lets it spin faster.
- But larger asteroids are ruled by gravity, not cohesion—so they must follow the 2-hour limit.
This means:
- Small asteroids can be “solid rocks” that spin fast.
- Large asteroids are “rubble piles” that must spin slower.

Food for thought: In this article, we explored a 2 body scenario and the intriguing ~2 hour orbital rule for rocky objects. But what if there are 3 bodies? Why does the universe follow such precise, predictable patterns for 2-body systems, while 3 or more bodies introduce chaos and extreme sensitivity to initial conditions?
What do you think? Making sense? Pretty simple eh!
Until we meet again!